math

Move objects in a circle smoothly

Some days ago, I posted an article called “Back to trigonometry” about moving objects in a circle by seconds, minutes or hours with a trigonometric formula.

Today I write about the making of my new watch face Burner.

Before writing about trigonometry again, I describe the production of the asset for moving in a circle.

Asset production of an animated gif video

I had the idea to move a flickering flame around a circle.

The first step, was to record a short gif video of the flame, which came out of my lighter. To do this, I simply used a GIF camera app. In my case, I’ve used Fixie GIF Camera.

Flame video

GIF video capture

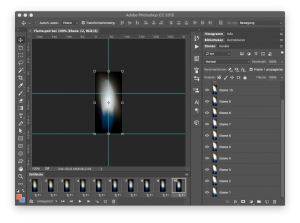
In default mode, this app records 10 frames, which was exactly what I needed. I imported it into Photoshop to crop it and center the single frames to the same position.

Unfortunately WatchMaker doesn’t support the transparent mode of animated gifs, so I had to choose a solid background color. Black was fine for my idea.

Moving the flame by seconds smoothly

I wanted to move the flame by seconds smoothly. As mentioned above, I used the same formula I’ve already described.

x = \cos((ds * \frac{1}{60} * 2 \pi) - \frac{\pi}{2})
y = \sin((ds * \frac{1}{60} * 2 \pi) - \frac{\pi}{2})

The problem by using the seconds as the input value is, that the flame moves step wise by seconds and not smoothly.

Update: Please use the formula in my new article Moving around – the easy way, because it’s better.

To move it smoothly, I’ve just added the thousands fraction of the millisecond of the current second. That’s all and looks like this:

x = \cos(((ds+\frac{dssz}{1000}) * \frac{1}{60} * 2 \pi) - \frac{\pi}{2})
y = \sin(((ds+\frac{dssz}{1000}) * \frac{1}{60} * 2 \pi) - \frac{\pi}{2})

In lua script it looks like this (here multiplied with 200 for a larger circle):

x="math.cos((({ds}+({dssz}/1000))*0.016666*math.pi*2)- math.pi/2) * 200"

y="math.sin((({ds}+({dssz}/1000))*0.016666*math.pi*2)- math.pi/2) * 200"

You can see the result in my watch face Burner.

Animation

Animation

Back to trigonometry

Since I’m scripting watch faces for smart watches, I was confronted with mathematical issues from my school days nearly 30 years ago.

The basics

The circle is the main geometric form to support using watch faces. And so I was confronted with π, sine, angles and some other things from the trigonometry.

Circle-trig6.svg

By This is a vector graphic version of Image:Circle-trig6.png by user:Tttrung which was licensed under the GFDL. Based on en:Image:Circle-trig6.png, which was donated to Wikipedia under GFDL by Steven G. Johnson. – This is a vector graphic version of Image:Circle-trig6.png by user:Tttrung which was licensed under the GFDL. ; Based on en:Image:Circle-trig6.png, which was donated to Wikipedia under GFDL by Steven G. Johnson., CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=770792

One main use for my watch faces so far, was, to move objects around a circle to a corresponding time value like I did with the eye movements of Homer in my Homer watch face or with the hours and minutes bobbles in TriGoIO.

I needed a function to place an object with the x and y coordinates in position of a circle to a given value of time. To do this, I needed sine, cosine and π.

Sine curve drawing animation.gif

By Lucas V. Barbosa – Own work, Public Domain, https://commons.wikimedia.org/w/index.php?curid=21360683

The seconds

To move Homer’s eyes by seconds, we use the WatchMaker variable {ds}, which represents the seconds in a minute from 0 to 60.

Because we want to calculate the x and y coordinates to place the object depending of the seconds, we need to use the sine and cosine functions.

As the illustration above shows, a full circle is 2 \pi.

To move an object around a circle we need values from 0 to 2 \pi, so we need to convert the 0 to 60 seconds to a value from 0 to 1 and multiply this with 2 \pi. So 60 seconds would be represented by 1 after the conversion which would result in 2 \pi when multiplied with 2 \pi, which is the full circle position.

To convert the seconds, we simple have to multiply them by \frac{1}{60}. The formula, where “ds” stands for the seconds, is: ds * \frac{1}{60} * 2 \pi.

To get the horizontal position in the clockwise movement we use the cosine function and we use the sine function for the vertical position.

x = \cos(ds * \frac{1}{60} * 2 \pi)
y = \sin(ds * \frac{1}{60} * 2 \pi)

Because the clock begins counting at the top of the watch face, we need to subtract \frac{\pi}{2} inside the cosine and sine functions.

x = \cos((ds * \frac{1}{60} * 2 \pi) - \frac{\pi}{2})
y = \sin((ds * \frac{1}{60} * 2 \pi) - \frac{\pi}{2})

That’s it.

Of course you can control the size of the circle by simply multiplying a desired value to it.
And if you wish to change the position of the circle, just add or subtract a value.
And if you would like to use hours, just use the {dh} variable and divide by 12 instead of 60.

Homer’s eyes

For Homer’s eyes in the Homer watch face, which have a specific size and position, I’ve used this formula:

Homer’s left eye:
x = -48 + \cos((ds * \frac{1}{60} * 2 \pi) - \frac{\pi}{2}) * 25
y = -42 + \sin((ds * \frac{1}{60} * 2 \pi) - \frac{\pi}{2}) * 25

Homer’s right eye:
x = 48 + \cos((ds * \frac{1}{60} * 2 \pi) - \frac{\pi}{2}) * 25
y = -42 + \sin((ds * \frac{1}{60} * 2 \pi) - \frac{\pi}{2}) * 25

The same in Lua script for WatchMaker as follows.

Tap on the object and set the values for “Position X” and “Position Y” to:

x="-48 + math.cos(({ds}*0.016666*math.pi*2)- math.pi/2) * 25"

y="-42 + math.sin(({ds}*0.016666*math.pi*2)- math.pi/2) * 25"

And for the other eye:

x="48 + math.cos(({ds}*0.016666*math.pi*2)- math.pi/2) * 25"

y="-42 + math.sin(({ds}*0.016666*math.pi*2)- math.pi/2) * 25"

Updates

Additional formula: Move objects in a circle smoothly
Alternative formula: Moving around – the easy way